SVM-p

إثبات معادلة الـ SVM

1. تعريف المعادلة الأساسية

احنا بنفترض إن المعادلة اللي بتمثل الـ Hyperplane هي:

$w\cdot x+b=0$

فين؟

• متجه عمودي على المستوي (الـ hyperplane) هو الw
• ال (bias) هو الb

2. ناخد نقطتين على المستوي

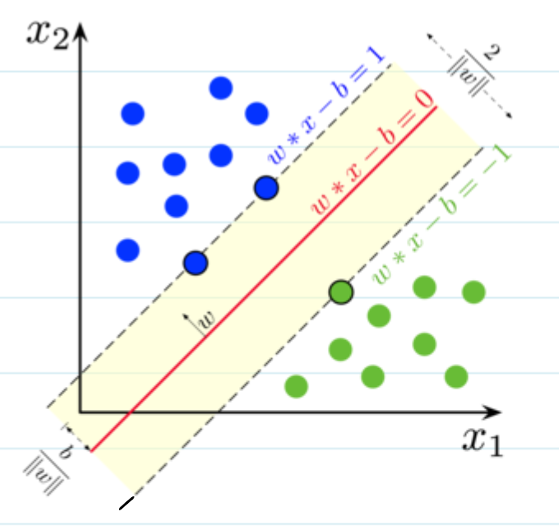بنختار أي نقطتين $x_1$ و $x_2$ موجودين على المستوي. بالتعويض في المعادلة:

$w\cdot x_1+b=0$ $w\cdot x_2+b=0$

لو طرحنا المعادلتين من بعض:

$w\cdot (x_1-x_2)=0$

وده معناه إن المتجه w عمودي (perpendicular) على المستوي

---

3. الشروط للعينات

بنفرض إن العينات بتتقسم لفئتين:

• العينات الموجبة (+):

$w\cdot x_i+b\ge 1$

• العينات السالبة (-):

$w\cdot x_i+b\le -1$

نقدر نجمع الشرطين في معادلة واحدة:

$y_i(w\cdot x_i+b)\ge 1$

• اللي بيوضح اذا كانت العينة موجبة (+1) او سالبة (-1) هو $y_i$

---

4. حساب الMargin Width

بنفترض إن الmargin هو المسافة بين المستويين اللي بيمثلوا حدود الفئات العرض (width) هو المسافة العمودية بين المستويين:

$\text{Width}=\frac{2}{||w||}$

هدفنا هنا هو تكبير الmargin، وده بيعادل تصغير $||w||$:

$\min \frac{1}{2}||w|{|}^2$

ليه بنستخدم التربيع؟ علشان يبقى التعامل اسهل للتبسيط لما نيجي نشتق قدام

---

5. حل باستخدام Lagrange Multipliers

علشان ناخد الconstraints في الاعتبار، بنستخدم طريقة Lagrange:

$L=\frac{1}{2}||w|{|}^2-{\sum }_{i=1}^l{\alpha }_i[y_i(w\cdot x_i+b)-1]$

فين؟

• ${\alpha }_i$: معاملات لاغرانج
• الشرط $y_i(w\cdot x_i+b)-1\ge 0$ محطوط جوا المعادله

6. اشتقاق القيم المثلى

اشتقاق بالنسبة لـ w:

$\frac{\partial L}{\partial w}=w-{\sum }_{i=1}^l{\alpha }_i{y}_i{x}_i=0$

لما نحلها:

$w={\sum }_{i=1}^l{\alpha }_i{y}_i{x}_i$

اشتقاق بالنسبة لـ b:

$\frac{\partial L}{\partial b}={\sum }_{i=1}^l{\alpha }_i{y}_i=0$