NN

Neural Networks

Origins

• Neural networks (NNs) are algorithms designed to mimic the brain.
• Popular in the 1980s and early 1990s, but popularity waned in the late 1990s.
• Recent resurgence as a state-of-the-art technique in various applications.
• Artificial neural networks are far simpler than the brain’s structure.

---

The Brain

• Composition: Networks of neurons.
• Function: Brain activity occurs due to neuron firing.
• Neurons:
  • Connect through synapses, propagating action potentials (electrical impulses).
  • Synapses release neurotransmitters, which can be:
    • Excitatory: Increase potential.
    • Inhibitory: Decrease potential.
  • Learning: Synapses exhibit plasticity, enabling long-term changes in connection strength.
• Scale:
  • ~10¹¹ neurons.
  • ~10¹⁴ synapses.

---

Neural Networks and the Brain

• Neural networks consist of computational models of neurons called perceptrons.

The Perceptron

• A threshold unit:
  • Fires if the weighted sum of inputs exceeds a threshold.
  • Analogous to a threshold gate in Boolean circuits.

graph TD
    Input1 -->|Weight1| Perceptron
    Input2 -->|Weight2| Perceptron
    Perceptron --> Output

Soft Perceptron (Logistic)

• Replaces threshold with a sigmoid activation function.
  • A “squashing” function that produces a continuous output.

---

Structure of Neural Networks

• Composed of nodes (units) connected by links.
  • Each link has a weight and activation level.
  • Each node has:
    • Input function: Summing weighted inputs.
    • Activation function: Transforms the input value.
    • Output.

Multi-Layer Perceptron

• Feed-Forward Process:
  1. Input layer units are activated by external stimuli (e.g., sensors).
  2. The input function computes input values by summing weighted activations.
  3. Activation function applies a non-linear transformation (e.g., sigmoid).
• Inputs: Real or Boolean.
• Outputs: Real or Boolean; can have multiple outputs per input.

graph LR
    Input1 --> Hidden1
    Input2 --> Hidden1
    Hidden1 --> Output
    Hidden1 --> Hidden2
    Hidden2 --> Output

---

Summary

• Neural networks are inspired by biological neurons but are far less complex.
• Their structure and functionality involve input, activation, and output, mimicking a simplified version of brain processes.
• Feed-forward networks like multi-layer perceptrons are foundational to many applications.

Slides Ex.2

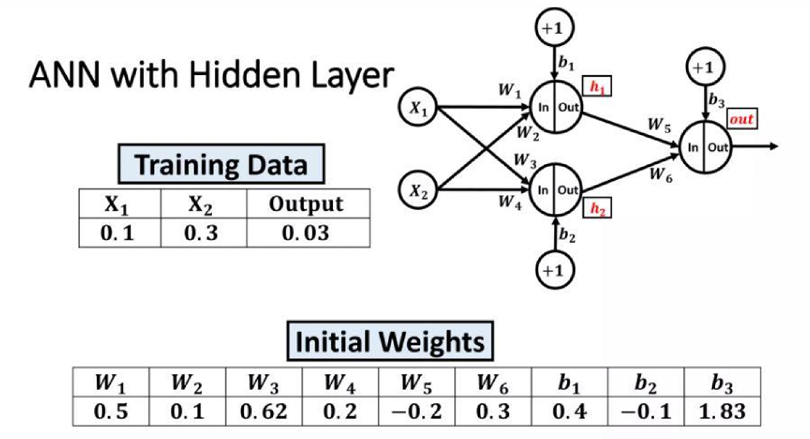
Error Function:

$E=\frac{1}{2}(y-out{)}^2$

1. Gradients for Output Layer Weights ($W_5,W_6$):

Let’s first compute the error gradient for $W_5$:

Step 1: Compute $\frac{\partial E}{\partial out}$:

$\frac{\partial E}{\partial out}=-(y-out)$

Step 2: Derivative of output activation:

For sigmoid:

\large out = f(z) = \frac{1}{1 + e^{-z}}$$$$\large f'(z) = out(1 - out)

$z=h_1{W}_5+h_2{W}_6+b_3$

$\frac{\partial out}{\partial z}=out(1-out)$

Step 3: Chain rule application:

For $W_5$:

$\frac{\partial E}{\partial W_5}=\frac{\partial E}{\partial out}\cdot \frac{\partial out}{\partial z}\cdot \frac{\partial z}{\partial W_5}$

Now substituting values:

1. $\frac{\partial z}{\partial W_5}=h_1$
2. $\frac{\partial out}{\partial z}=out(1-out)$

$\frac{\partial E}{\partial W_5}=-(y-out)(out)(1-out)(h_1)$

Similarly, for $W_6$:

$\frac{\partial E}{\partial W_6}=-(y-out)(out)(1-out)(h_2)$

---

2. Gradients for Hidden Layer Weights ($W_1,W_2,W_3,W_4$):

For $W_1$ (connected to $h_1$):

We need to backpropagate through $h_1$:

$\frac{\partial E}{\partial W_1}=\frac{\partial E}{\partial out}\cdot \frac{\partial out}{\partial z}\cdot \frac{\partial z}{\partial h_1}\cdot \frac{\partial h_1}{\partial z_1}\cdot \frac{\partial z_1}{\partial W_1}$

Breaking it down:

1. From earlier:

$\frac{\partial E}{\partial out}=-(y-out),\frac{\partial out}{\partial z}=out(1-out)$

2. From hidden layer $h_1$:

$\frac{\partial h_1}{\partial z_1}=h_1(1-h_1)$

3. Weight contribution:

$\frac{\partial z_1}{\partial W_1}=X_1$

Combining:

$\frac{\partial E}{\partial W_1}=-(y-out)(out)(1-out)(W_5)(h_1)(1-h_1)(X_1)$

Similarly, for $W_2$:

$\frac{\partial E}{\partial W_2}=-(y-out)(out)(1-out)(W_5)(h_1)(1-h_1)(X_2)$

---

3. Final Gradient Formulas:

• Output Layer:

\large \frac{\partial E}{\partial W_5} = -(y - out)(out)(1 - out)(h_1)$$$$\large \frac{\partial E}{\partial W_6} = -(y - out)(out)(1 - out)(h_2)

• Hidden Layer:

\large \frac{\partial E}{\partial W_1} = -(y - out)(out)(1 - out)(W_5)(h_1)(1 - h_1)(X_1)$$$$\large \frac{\partial E}{\partial W_2} = -(y - out)(out)(1 - out)(W_5)(h_1)(1 - h_1)(X_2)$$$$\large \frac{\partial E}{\partial W_3} = -(y - out)(out)(1 - out)(W_6)(h_2)(1 - h_2)(X_1)$$$$\large \frac{\partial E}{\partial W_4} = -(y - out)(out)(1 - out)(W_6)(h_2)(1 - h_2)(X_2)